Théorème de Thalès - triangles semblables - homothéties - agrandissement/réduction

Exemple 1:



Sur la figure ci-dessus, on peut remarquer que:
  • Le segment [A'B'] est l'image du segment [AB] par l'homothétie de centre O et de rapport -3.
  • Les triangles ABO et A'B'O vérifient les conditions du théorème de Thalès:
    • les points A, O, A' sont alignés
    • les points B, O, B' sont alignés
    • les droites (AB) et (A'B') sont paralléles
    • les rapports de Thalès sont égaux: AB/ A'B'=AO/A'O=BO/B'O
  • Les triangles ABO et A'B'O sont semblables:
    • leurs longueurs sont proportionnelles:
      • A'B'=3AB
      • A'O=3AO
      • B'O=3BO
    • leurs angles sont deux à deux égaux
    • le triangle A'B'O est un agrandissement du triangle ABO

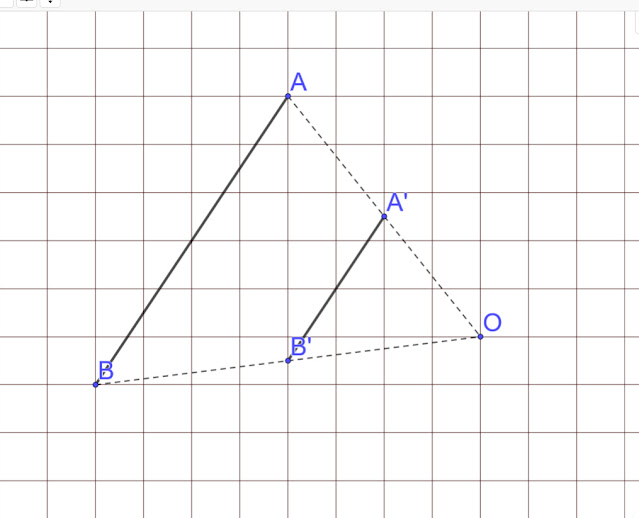
Exemple 2:


Sur la figure ci-dessus, on peut remarquer que:
  • Le segment [A'B'] est l'image du segment [AB] par l'homothétie de centre O et de rapport 0,5.
  • Les triangles ABO et A'B'O vérifient les conditions du théorème de Thalès:
    • les points O, A, A' sont alignés
    • les points O, B,  B' sont alignés
    • les droites (AB) et (A'B') sont paralléles
    • les rapports de Thalès sont égaux: AB/ A'B'=AO/A'O=BO/B'O
  • Les triangles ABO et A'B'O sont semblables:
    • leurs longueurs sont proportionnelles:
      • A'B'=0,5AB
      • A'O=0,5AO
      • B'O=0,5BO
    • leurs angles sont deux à deux égaux
    • le triangle A'B'O est une réduction du triangle ABO

Exercices à rendre:

Fais proprement dans ton cahier les exercices 45 p 191 et 48 p 191
puis prend ta feuille en photo et envoie ton travail au professeur en passant par l'ENT ou en envoyant un mail à: stephane.grosset@ac-reunion.fr